本文树、二叉树部分系阅读《数据结构(C语言版)》,严蔚敏等著一书中第六章 树和二叉树部分章节的笔记。树形结构是一类重要的非线性数据结构,直观看来,树是以分支关系定义的层次结构。树结构在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可用树来形象表示。树在计算机领域中也得到广泛应用,如在编译程序中,可用树来表示源程序的语法结构。又如在数据库系统中,树形结构也是信息的重要组织形式之一。本章重点讨论二叉树的存储结构及其各种操作,并研究树和森林与二叉树的转换关系。
树的定义和基本术语
树是n(n>=0)个结点的有限集,在任意一棵非空树中:
- 有且仅有一个特定的根(root)结点
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2…Tm,其中每一个集合本身又是一棵树,并且称为根的子树。如下图所示,(a)是只有一个根结点的树;(b)是有13个结点的树,其中A是根,其余结点分成3个互不相交的子集:T1={B,E,F,K,L}、T2={C,G}、T3={D,H,I,J,M},T1、T2、T3都是根A的子树,且本身也是一棵树
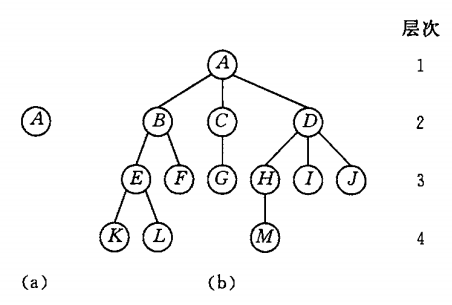
树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的度,上图(b)中,A的度为3,C的度为1,F的度为0。度为0的结点称为叶子或终端结点,结点K、L、F、G、M、I、J都是树的叶子。度不为0的结点称为非终端结点或分支结点,除根结点外,分支结点也称为内部结点。树的度是树内各结点的度的最大值,图(b)中树的度为3。
结点的子树的根称为该结点的孩子,相应的,该结点称为孩子的双亲。图(b)中D为A的子树T3的根,则D是A的孩子,而A是D的双亲,同一个双亲的孩子之间互称兄弟,例如,H、I和J互为兄弟。结点的祖先是从根到该结点所经分支上的所有结点,M的祖先为A、D、H,反之,以某结点为根的子树中的任一结点都称为该结点的子孙,B的子孙为E、K、L、F。
结点的层次从根开始定义起,根为第一层,根的孩子为第二层。双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度或高度,图(b)中树的深度为4。
如果将树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。在有序树中最左边的子树的根称为第一个孩子,最右边的称为最后一个孩子。
森林是m棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
二叉树
定义
二叉树是另一种树型结构,它的特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。二叉树可以有5种基本形态:空二叉树、仅有根结点的二叉树、右子树为空的二叉树、左右子树均非空的二叉树、左子树为空的二叉树。
性质
二叉树具有下列重要特性:
- 在
二叉树的第i层上至多有2^(i-1)个结点(i>=1) 深度为k的二叉树至多有(2^k)-1个结点(k>=1)- 对任何一棵
二叉树T,如果其终端结点/叶子数为n0,度为2的结点数为n2,则n0=n2+1
一棵深度为k且有(2^k)-1个结点的二叉树称为满二叉树,这种树的特点是每一层上的结点数都是最大结点数,如下图(a)中所示。
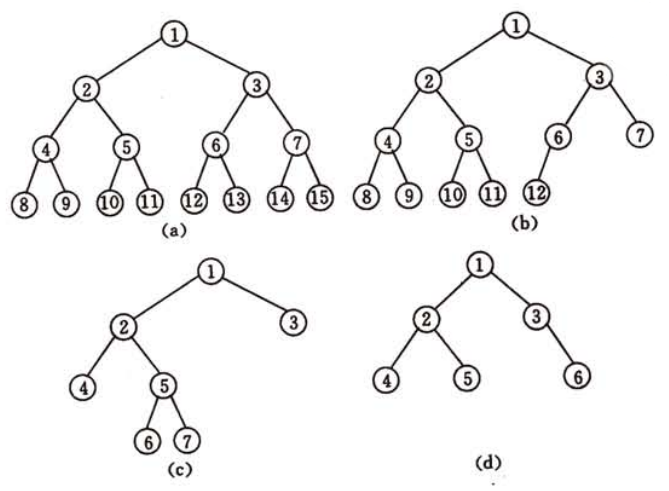
对满二叉树的结点进行连续编号,约定编号从根结点起,自上而下,自左至右,由此可引出完全二叉树的定义。深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一 一对应时,称之为完全二叉树。这种树的特点是:叶子结点只可能在层次最大的两层上出现;对任一结点,若其右分支下的子孙的最大层次为L,则其左分支下的子孙的最大层次必为L或L+1。下图中(b)是完全二叉树,而(c)、(d)不是完全二叉树。
- 具有n个结点的
完全二叉树的深度为[lgn/lg2]+1,其中,[x]表示不大于x的最大整数 - 如果对一棵有n个结点的
完全二叉树(其深度为[lgn/lg2]+1)的结点按层序编号(从第1层到第[lgn/lg2]+1层,每层从左到右),则对任一结点i(1=<i<=n),有- 如果i=1,则结点i是
二叉树的根,无双亲;如果i>1,则其双亲PARENT(i)是结点[i/2] - 如果2i>n,则结点i无左
孩子(结点i为叶子结点);否则其左孩子LCHILD(i)是结点2i - 如果2i+1>n,则结点i无右
孩子;否则其右孩子RCHILD(i)是结点2i+1
- 如果i=1,则结点i是
存储结构
顺序存储结构
按照顺序存储结构的定义,在此约定,用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为 i 的结点元素存储在如上定义的一维数组中下标为 i-1 的分量中。这种顺序存储结构仅适用于完全二叉树,因为在最坏的情况下,一个深度为k且只有k个结点的单支树(树中不存在度为2的结点)却需要长度为(2^k)-1。
链式存储结构
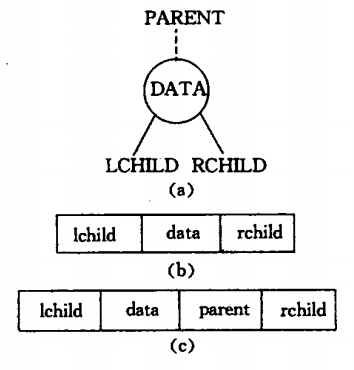
设计不同的结点结构可构成不同形式的链式存储结构。由二叉树的定义得知,二叉树的结点,如下图a所示,由一个数据元素和分别指向其左、右子树的两个分支构成,则表示二叉树的链表中的结点至少包含3个域:数据域和左、右指针域,如下图b所示。有时,为了便于找到结点的双亲,则还可在结点结构中增加一个指向其双亲结点的指针域,如下图c所示。
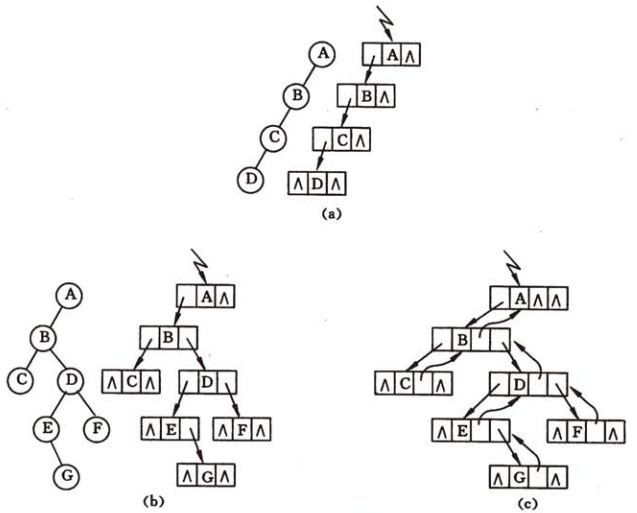
利用这两种结点结构所得二叉树的存储结构分别称之为二叉链表和三叉链表,如下图所示。链表的头指针指向二叉树的根结点,容易证得,在含有n个结点的二叉链表中有n+1个空链域。
B-Tree
B-Tree是一种平衡的多路查找树,一棵m阶的B-Tree,或为空树,或为满足下列特性的m叉树:
- 树中每个结点至多有m棵子树
- 若根结点不是
叶子结点,则至少有两棵子树 - 除根之外的所有
非终端结点至少有[m/2]向上取整棵子树 - 所有的
非终端结点中包含下列信息数据:(n,P0,K1,P1,K2,P2,……,Kn,Pn)- Ki (i=1…n)为关键字,且Ki < K(i+1) (i=1…n-1)
- Pi (i=0…n)为指向子树根结点的指针,且指针P(i-1)所指子树中所有结点的关键字均小于Ki (i=1…n),Pn所指子树中所有结点的关键字均大于Kn
- n ([m/2]-1 <= n <= m-1)为关键字的个数,或n+1为子树个数
- 所有的
叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)
备注:此处的[x]表示不小于x的最小整数,向上取整。如下图所示,m=4:
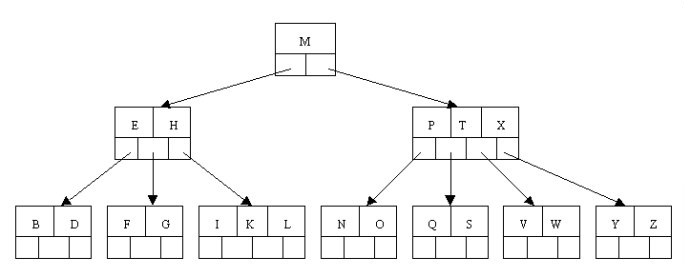
B-Tree文件查找的具体过程示例如下(涉及磁盘I/O操作):
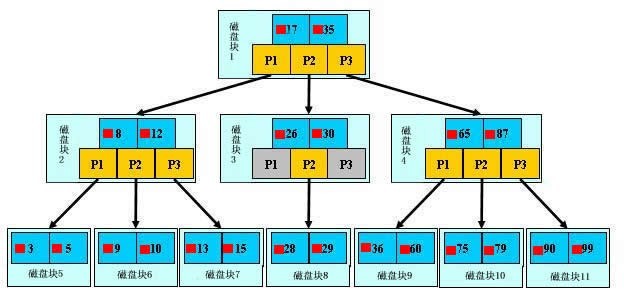
此处用少量的数据构造一棵三叉B-Tree,实际应用中B-Tree结点的关键字很多。上图中,17表示磁盘文件的文件名,红色方块表示文件17的内容在硬盘中的存储位置,P1表示指向文件17左子树的指针。假设每个盘块恰好可以存放一个B-Tree的结点(可以存放两个文件名),下面模拟查找文件29的过程:
- 根据根结点指针找到文件目录的根磁盘块1,将其中的信息导入内存。 [磁盘I/O操作1次]
- 此时内存中有17、35两个文件名和三个存储其它磁盘页面地址的数据,17<29<35,因此找到指针P2
- 根据P2指针定位到磁盘块3,并将其中的信息导入内存。 [磁盘I/O操作2次]
- 此时内存中有26、30两个文件名和三个存储其他磁盘页面地址的数据,26<29<30,因此找到指针P2
- 根据P2指针,定位到磁盘块8,并将其中的信息导入内存。 [磁盘I/O操作3次]
- 此时内存中有28,29两个文件,查找到29文件,并定位该文件内存的磁盘地址
分析上述过程,需要3次磁盘I/O操作和3次内存查找操作。关于内存中的文件名查找,由于是一个有序表结构,可以利用折半查找提高效率,I/O操作是影响整个B-Tree查找效率的决定因素。
B+Tree
B+Tree是应文件系统所需而产生的一种B-Tree的变型树,一棵m阶的B+Tree和一棵m阶的B-Tree的差异在于:
B+Tree中有n棵子树的结点中含有n个关键字;B-Tree中有n棵子树的结点中含有n-1个关键字- 所有的
叶子结点中包含了全部关键字信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接;B-Tree的叶子结点并不包含全部需要查找的信息 - 所有的
非终端结点可以看成是索引部分,结点中仅含有其子树根结点的最大(或最小)关键字;B-Tree的非终端结点也包含需要查找的信息
如下图所示,m=3:
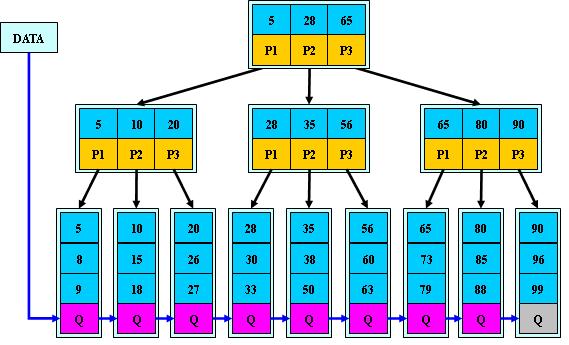
通常在B+Tree上有两个头指针,一个指向根结点,另一个指向关键字最小的叶子节点。因此,可以对B+Tree进行两种查找运算:一种是从最小关键字起顺序查找,另一种是从根结点开始,进行随机查找。
索引中使用B+Tree而非B-Tree的原因
B+Tree的磁盘读写代价更低。B+Tree的内部结点并没有指向关键字具体信息的指针,因此其内部结点相对B-Tree更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存中的需要查找的关键字也就越多,相对来说,I/O读写次数也就降低了B+Tree的查询效率更加稳定。由于非终端结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引,所以任何关键字的查找必须走一条从根结点到叶子结点的路,所有关键字查询的路径长度相同,每一个数据的查询效率相当
B*Tree
B*Tree是B+Tree的变体,在B+Tree的非根和非叶子结点上增加指向兄弟结点的指针,如下图所示
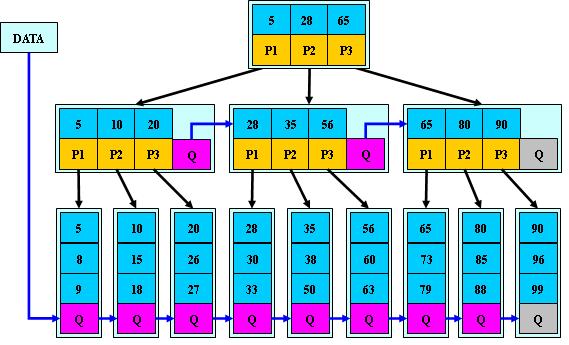
B*Tree定义了非叶子结点关键字个数至少为(2/3)*m,即块的最低使用率为2/3(代替B+Tree的1/2)。
B+Tree的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+Tree的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。
B*Tree的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟结点也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
B*Tree分配新结点的概率比B+Tree要低,空间使用率更高。